Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Principi generali di analisi acustica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-J01 - Acustica - Pag. ATS-J01.04
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2025- e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Analisi in frequenza: Forza armonica semplice
Si definisce armonica semplice una forza f(t) che possiede legge armonica e ampiezza unitaria.
Questa condizione è soddisfatta dalle espressioni reali f(t) = sin
wt o f(t) = cos wt e dall’espressione complessa f(t) = eiwt.
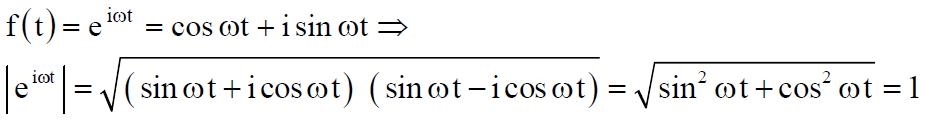
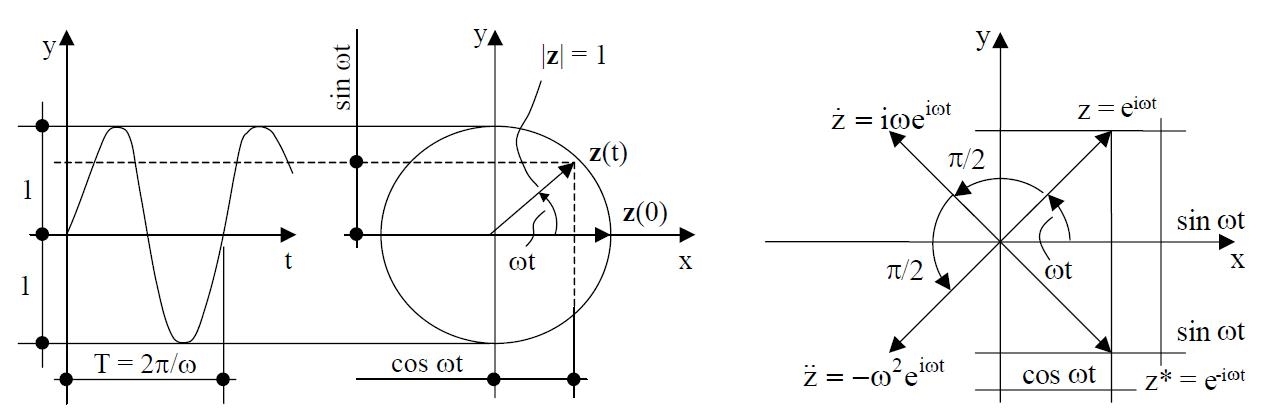
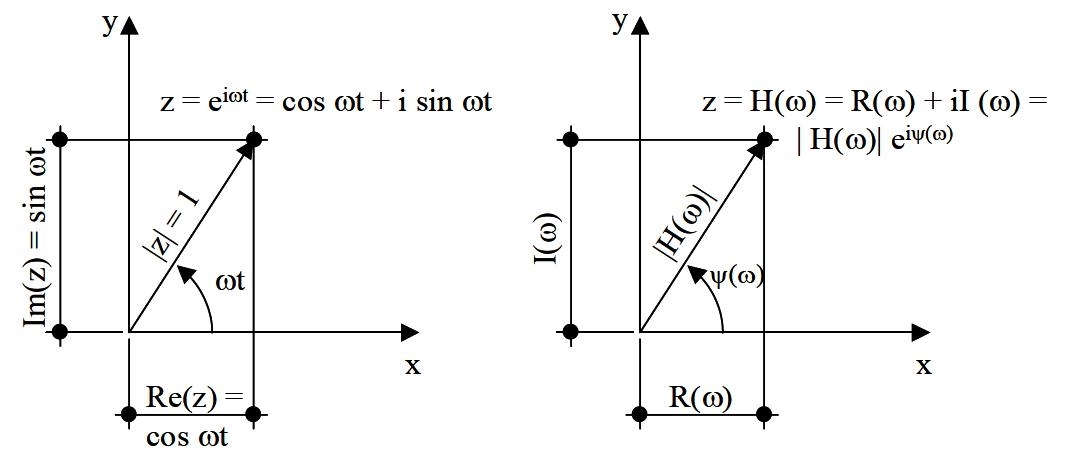
Osservazione: La funzione armonica sin ωt può essere considerata la proiezione sull’asse y delle ordinate di un vettore Z di modulo unitario, ruotante intorno all’origine di un sistema di riferimento cartesiano (x, y) con velocità angolare costante ω e fase iniziale nulla. Ragionamento analogo può essere fatto per la funzione armonica cos ωt relativamente alla proiezione sull’asse x delle ascisse.
Interpretando il piano (x, y) come piano di Argand-Gauss, al vettore Z viene associato un valore complesso z le cui parti reale e immaginaria sono rispettivamente le proiezioni su x e su y di Z : z=x + iy, x = Re(z) = cos ωt, y = Im(z) = sin ωt, e pertanto z = cos ωt + i sin ωt.
Applicando la formula di Eulero z = eiwt.
Si prenda in esame l’equazione del moto:
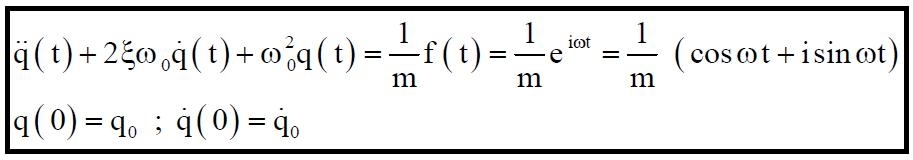 (01)
(01)
Poiché f(t) è una grandezza complessa, anche q(t) è una grandezza complessa. Si pone:
q(t) = x(t) + i y(t)
nella quale le funzioni reali x(t) = Re[q(t)], y(t) = Im[q(t)] sono rispettivamente le soluzioni dei due seguenti problemi:
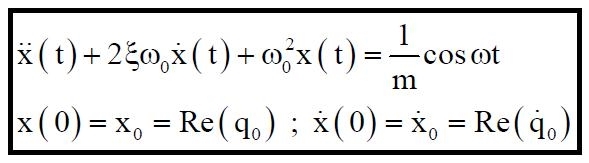 (02)
(02)
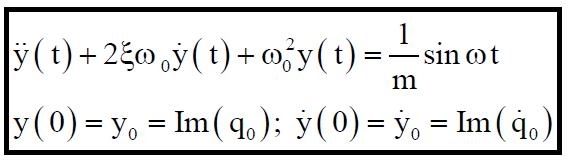 (03)
(03)
Si constata che la risposta y(t) alla forza armonica semplice reale f(t) = sin ωt è la parte immaginaria della risposta q(t) alla forza armonica semplice complessa f(t) = eiwt.
La soluzione della (01) è data dalla somma dell’integrale q' (t) dell’omogenea associata e di un qualsiasi integrale particolare q'' (t) della completa:
q (t) = q' (t) + q'' (t).
Dalle precedenti si ricava:
q' (t) = x' (t) + i y' (t) x (t) = x' (t) + x'' (t)
q'' (t) = x'' (t) + i y'' (t) y (t) = y' (t) + y'' (t)
dove x' (t) e y' (t) e sono gli integrali delle omogenee associate alla (02) e alla (03):
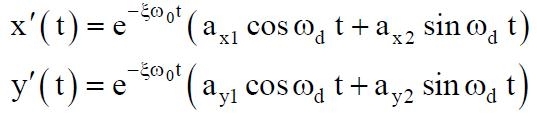
Le costanti di integrazione sono associate alle condizioni iniziali.
Si dimostra che un integrale particolare q'' (t) della (01) è:
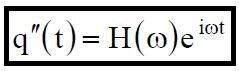 (04)
(04)
Sostituendo infatti la (04) nella (01) risulta:
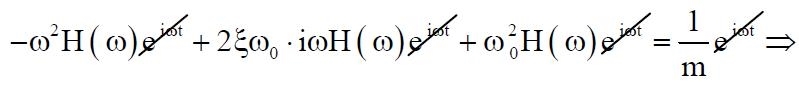
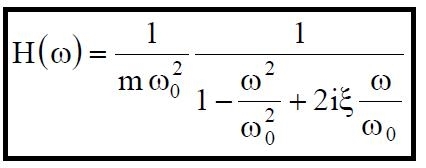 (05)
(05)
H(ω) è definita funzione di risposta complessa in frequenza.
La grandezza complessa H(ω) può essere riscritta nelle forme:
![]() (06)
(06)
![]() (07)
(07)
nelle quali:
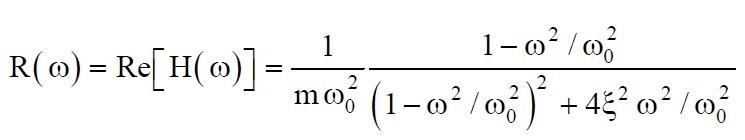 (08)
(08)
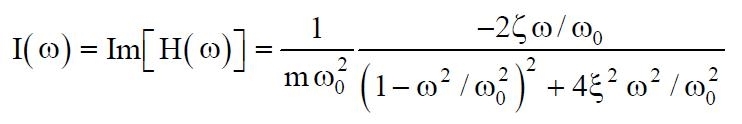 (09)
(09)
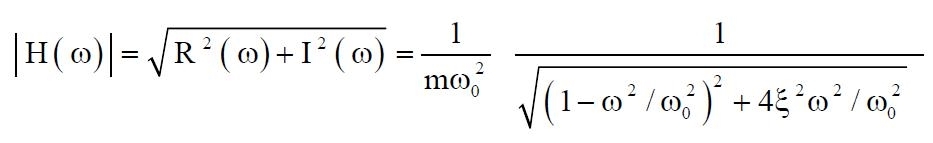 (10)
(10)
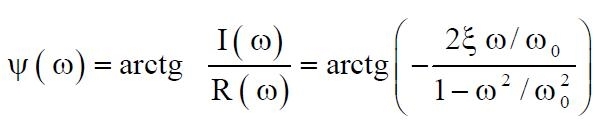 (11)
(11)
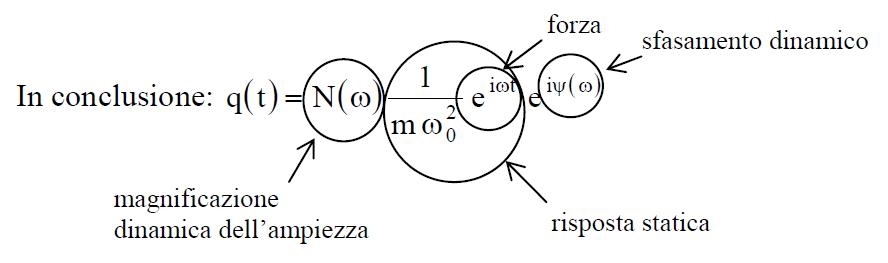
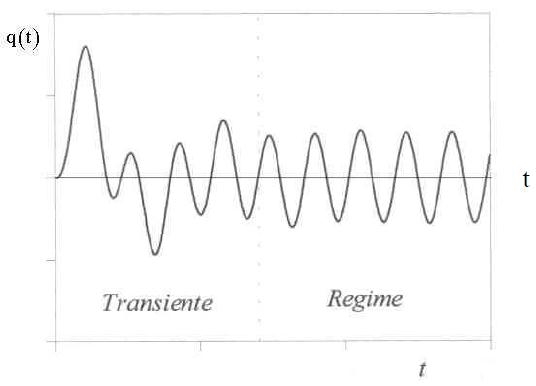
In ipotesi di vibrazioni a regime q' (t) = 0 allora: q (t) = q'' (t) allora: q (t) = H(ω) eiω t (12).
La (12) esprime la risposta a regime di un sistema sottoposto a una forza armonica semplice complessa f(t) = eiω t. Rivela inoltre il significato fondamentale della funzione H(ω): in condizioni di vibrazioni a regime, per forza armonica semplice, è il rapporto fra la risposta e l’eccitazione.
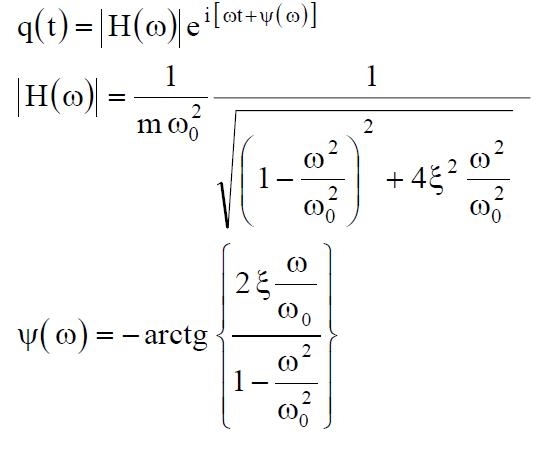
Sostituendo la (07) nella (12) si ottiene:
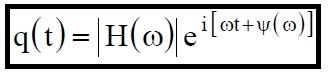 (13)
(13)
Se ne deduce che | H(ω) | è l’ampiezza del moto vibratorio ψ (ω) è il ritardo di fase della risposta q(t) rispetto all’eccitazione f(t) = eiω t.
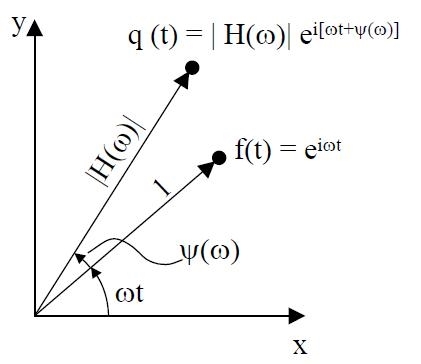
f(t) = eiω t
Þ
per ω = 0

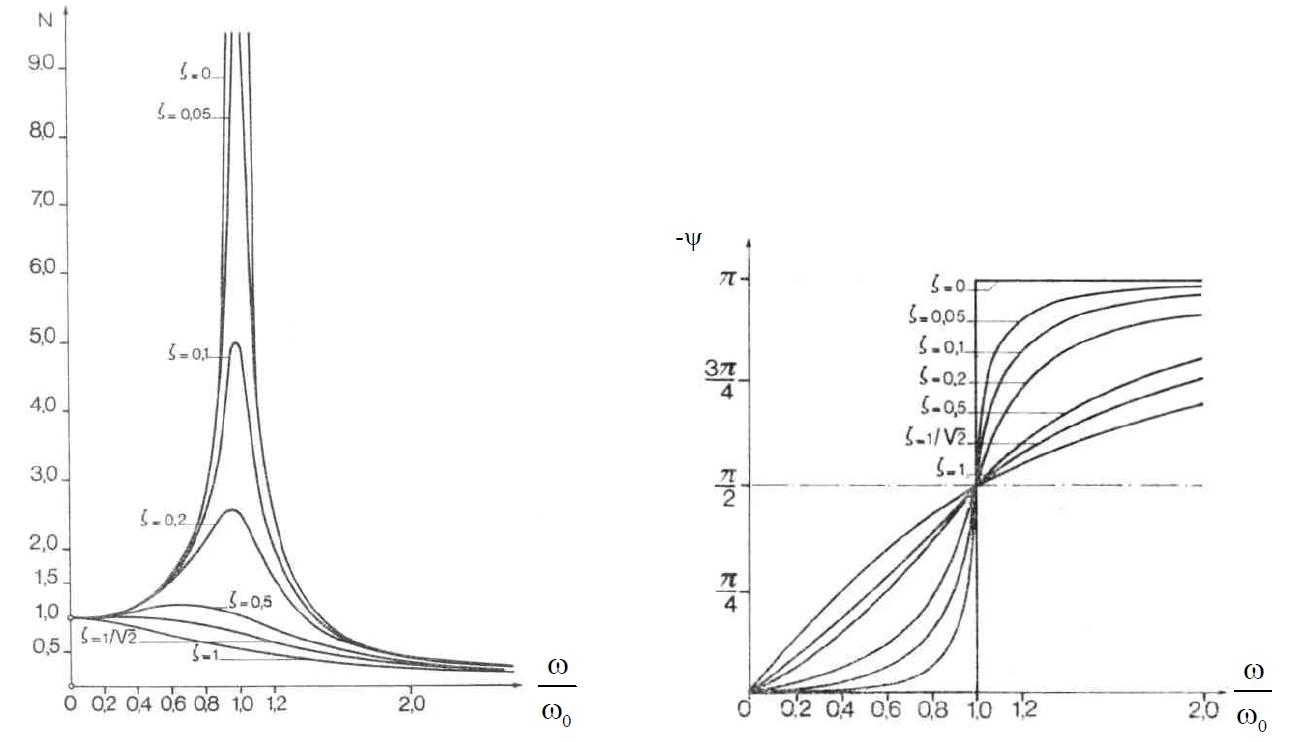
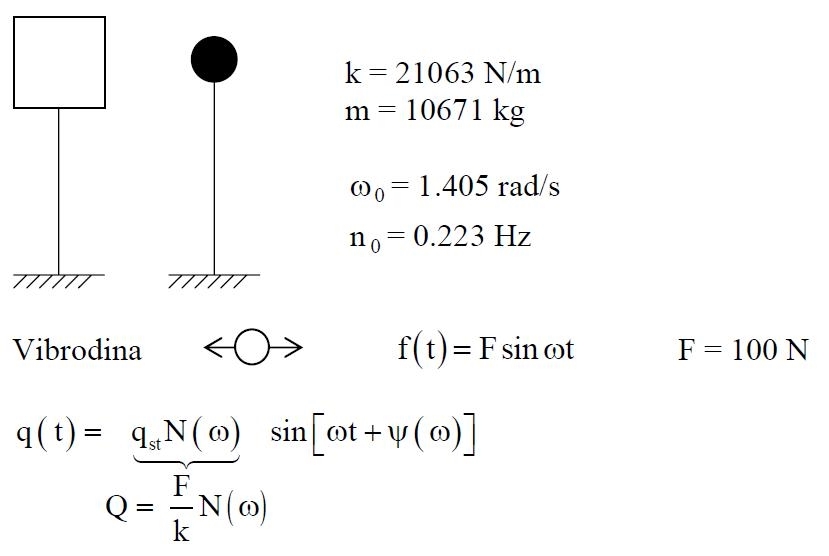
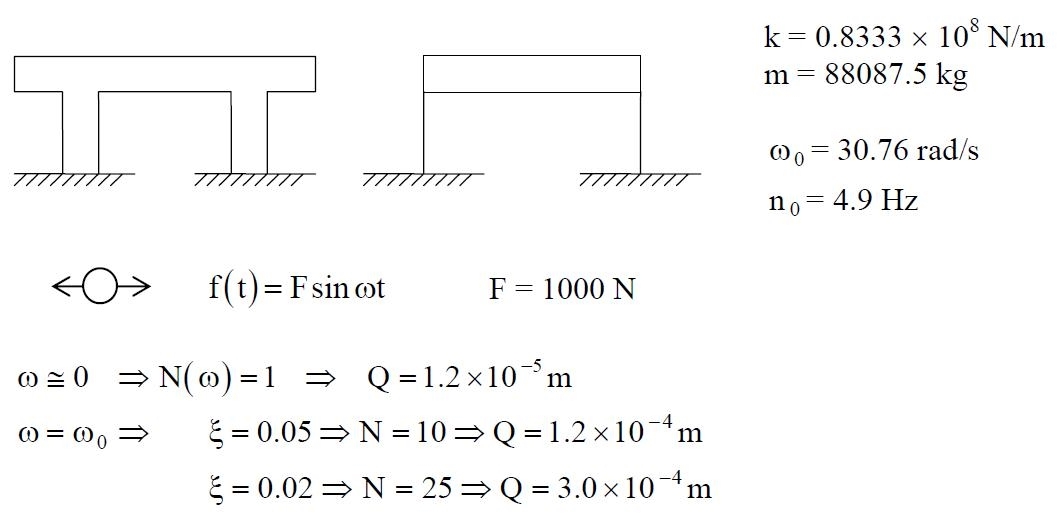
Si definisce fattore di magnificazione N(ω) il rapporto fra l’ampiezza | H (ω) | della risposta dinamica e l’ampiezza H(0) della risposta statica:
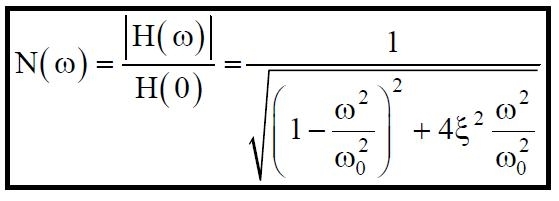 (14)
(14)

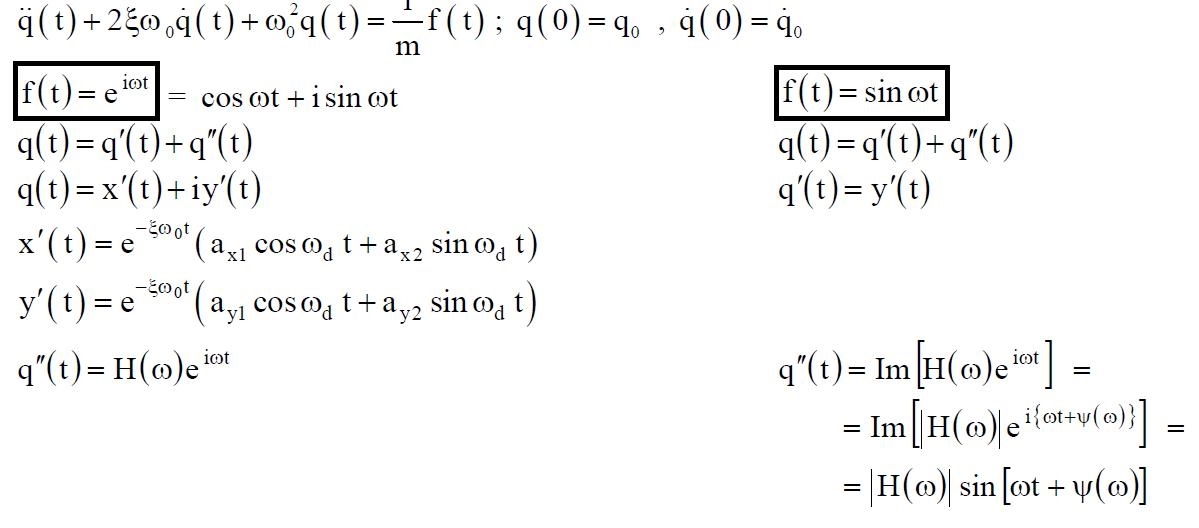

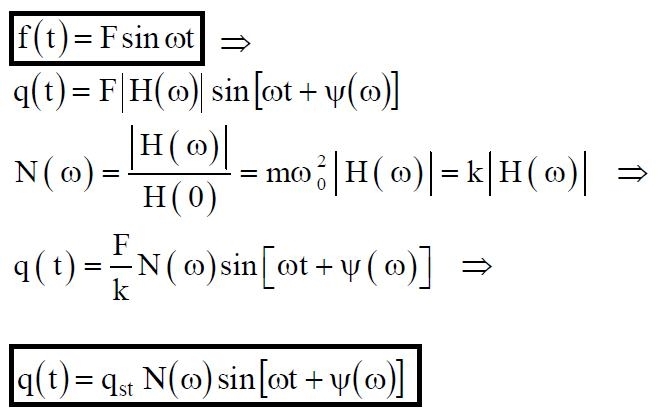
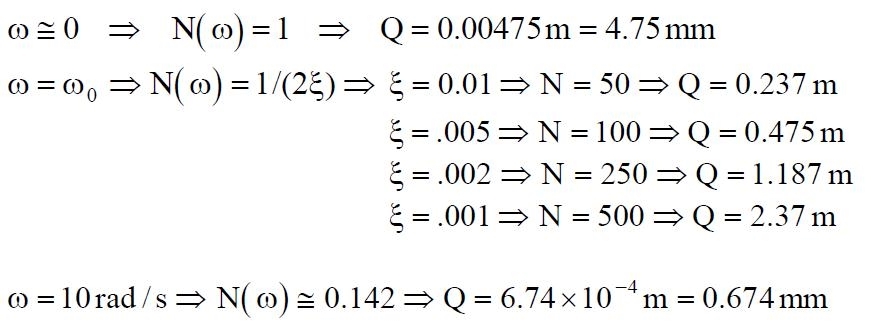
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-067 - Ing. Arch. Michele Cuzzoni - Appunti di Fisica 2: Acustica – Facoltà di Ingegneria, Pavia - A.A. 1995-1996
Bib-TS-068 - Il Nuovo Colombo - Manuale dell'Ingegnere - Volume primo - 83^ edizione - Ed. Ulrico Hoepli Milano - 1997 Ristampa 2001