Portale "Ingegneria e Campanologia" - Autore - Sommario - Mappa del Sito - Home
Strutturistica Chimica
AREA I - ARTE TECNICO-SCIENTIFICA (ATS)
Cap. ATS-F02 - Chimica - Pag. ATS-F02.12
Gli argomenti trattati sono stati inseriti da Ing. Arch. Michele Cuzzoni nel 2012 - © Copyright 2007- 2024 - e sono desunti dalla documentazione indicata in Bibliografia a fondo pagina
Traslazione
: operazione che non riorienta un oggetto ma lo sposta di un multiplo di un vettore (reticolare).In termini geometrici in termini matriciali (somma di vettori)
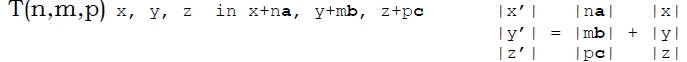
genera operazioni composte da una rotazione propria ed una traslazione di una frazione di un vettore traslazionale.
· Angolo di rotazione e = 360°/X (X = 1, 2, 3, 4, 6)
· Traslazione di un vettore s parallelo all’asse t (di lunghezza t), dove s è la componente elicogira.
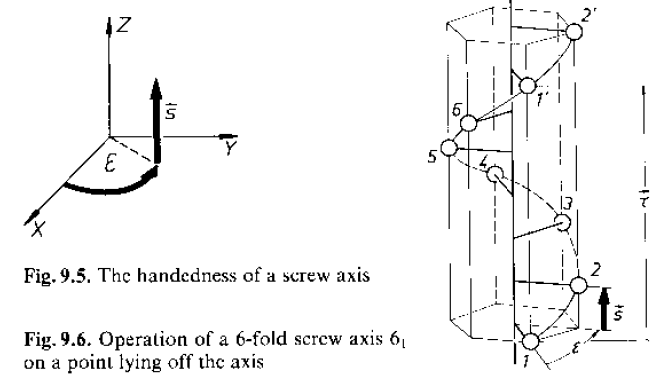
· Si dimostra che s può valere solo 0, t/X, 2t/X, … (X-1)t/X;
· Le diverse operazioni indipendenti sono X0, X1, X2, …XX-1
Ovviamente X0 = X;
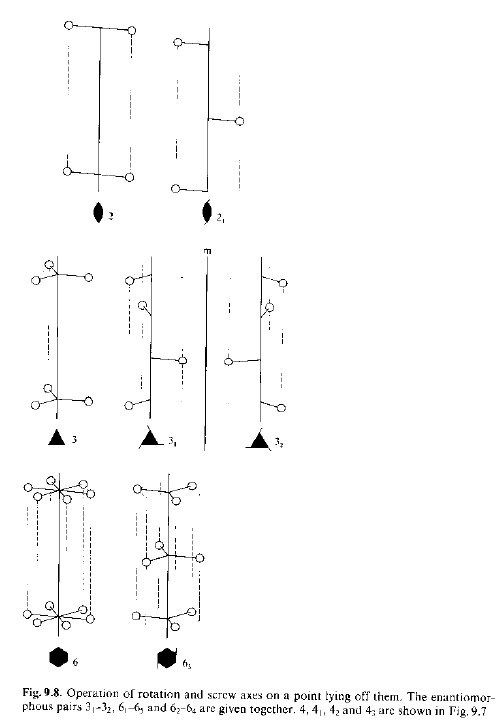
· Per assi elicogiri binari esiste solo 21;
· Per assi elicogiri ternari esistono solo 31 e 32; 31 e 32 sono mutuamente enantiomorfi.
· Per assi elicogiri quaternari esistono solo 41, 42, 43; 41 e 43 sono mutuamente enantiomorfi.
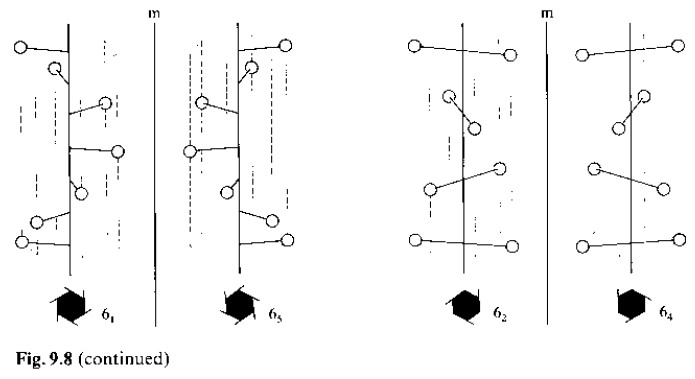
· Per assi elicogiri senari esistono solo 61, 62, 63, 64, 65;
61 e 65 sono mutuamente enantiomorfi.
62 e 64 sono mutuamente enantiomorfi.
In termini matriciali: x’ = Mx + s (rotazione + traslazione)
Genera operazioni composte da una riflessione propria ed una traslazione di una frazione di un vettore traslazionale.
· Riflessione
· Traslazione di un vettore g parallelo al piano glide, dove g è la componente di scorrimento.
Tipicamente, g è metà della traslazione di reticolo parallela al piano glide, ovvero g = ½
t
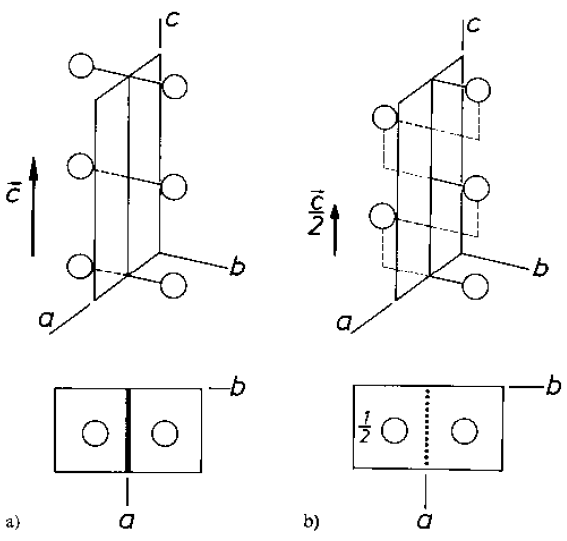
Piano glide di tipo a: riflessione normale ad un piano con traslazione di ½ a.
Piano glide di tipo b: riflessione normale ad un piano con traslazione di ½ b.
Piano glide di tipo c: riflessione normale ad un piano con traslazione di ½ c.
Esempio di Piano glide di tipo n: (diagonale) riflessione normale ad un piano con traslazione di ½ (a+b).
Esempio di Piano glide di tipo d: (diamond, raro) riflessione normale ad un piano con traslazione di ¼
(t1+t2).
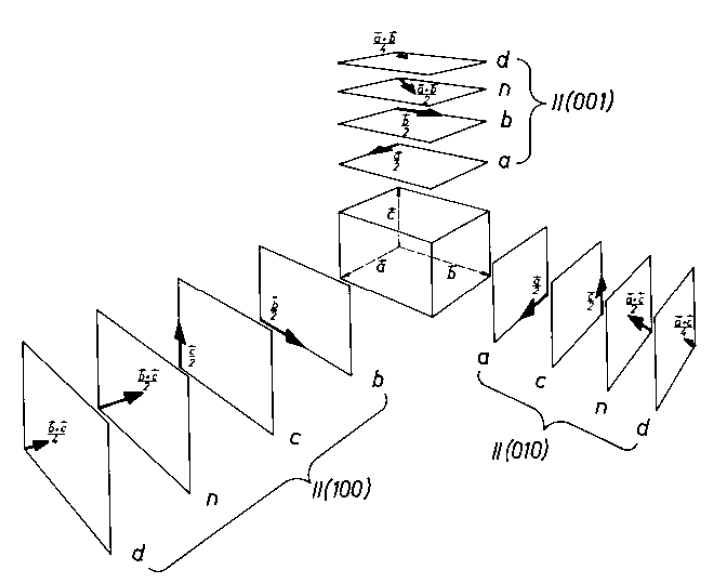
In termini matriciali: x’ = Mx + g (riflessione + traslazione)
Combinando i 32 gruppi puntuali con
i 14 Reticoli di Bravais (ovvero associando alle operazioni puntuali le operazioni di traslazione) si possono ottenere 230 Gruppi Spaziali (e non 32 x 14 = 448!).I gruppi spaziali, determinati indipendentemente da Fedorov (Mosca,), Sohncke (Monaco), Schönflies (Gottinga) e Barlow (Londra) verso la fine del 1800, sono veri gruppi matematici che contengono simmetrie puntuali, traslazionali e composte (assi screw e piani glide).
Qualsiasi sistema 3D ordinato DEVE appartenere ad uno delle 230 tipologie possibili, così come in 2D erano possibili solamente 17 gruppi planari.
I diversi gruppi spaziali indicano la relazione reciproca di motivi nello spazio, senza definire la forma e l’orientazione del motivo di base.
P.es. AgClO4 ed urea NH2CONH2 mostrano lo stesso gruppo spaziale (I-4m2) ma strutture (motivi molecolari o ionici) completamente diverse!
L’intera catalogazione è distribuita dalle Tabelle Internazionali per le Cristallografia, che utilizza la simbologia di Herrmann-Mauguin.
Il simbolo H-M contiene dapprima una lettera maiuscola, che individua il reticolo di Bravais: P, C, I, F, R (qualche volta, per diversa orientazione degli assi appaiono anche A e B).
Seguono poi 1, 2 o 3 campi (numeri o lettere) che descrivono elementi di simmetria minimali (detti generatori), che per loro composizione, assieme al tipo di reticolo, permettono di generare l’insieme completo delle operazioni di simmetria del gruppo.
Esempi:
P –1 indica un gruppo spaziale triclino (ovviamente primitivo) che contiene un centro di simmetria. L'unico altro gruppo spaziale triclino è P 1 (acentrico).
P 2/m indica un gruppo spaziale monoclino primitivo, che possiede un asse binario perpendicolare ad un piano di riflessione (e quindi generano un centro). Suoi sottogruppi propri sono P 2 (acentrico), P m (acentrico) e P –1 (triclino, centrico!), a seconda che io rimuova, delle quattro operazioni iniziali [E, -1, 2, m] le coppie (-1,m), (-1,2) o (2,m).
C 2/m è un gruppo spaziale che contiene [E, -1, 2, m] + altre quattro operazioni generate dalla traslazione di reticolo C +1/2(a+b).
P 21/c
indica in gruppo spaziale monoclino primitivo, in cui sono presenti un asse elicogiro binario ed un piano di scorrimento perpendicolare ad esso, con traslazione di ½ c.La combinazione di questi due elementi genera un centro di simmetria (-1) che non sta né sul piano né sull’asse.
Sottogruppi propri sono
P 21 (acentrico), P c (acentrico) e P–1 (triclino, centrico!), a seconda che io rimuova, delle quattro operazioni iniziali [E, -1, 21, c] le coppie (-1,c), (-1,21) o (21/c).P b c n è un gruppo spaziale ortorombico primitivo, che possiede un piano di scorrimento di tipo b perpendicolare ad a, un piano di scorrimento di tipo c perpendicolare a b, ed un piano di scorrimento diagonale n perpendicolare a c. Questi generatori implicano anche la presenta di centri di inversione (-1) ed assi binari propri od elicogiri. L’insieme delle otto operazioni di simmetria che fanno gruppo pertanto è:
[E, 21(a), 2(b), 21(c), -1, b(^a), c(^b), n(^c)]
Il simbolo H-M esteso è P 21/b 2/c 21/n
P 42 2 2 è un gruppo spaziale tetragonale primitivo che possiede un asse elicogiro 42 (lungo z) ed assi binari sia lungo gli assi coordinati (x e y) che lungo le bisettrici dei quadranti (rette y = x e y = -x). La combinazione di questi elementi NON genera centri di simmetria. Il gruppo è acentrico.
P 63 m c
è un gruppo esagonale (acentrico) che possiede un asse elicogiro 63 (lungo z), un piano di riflessione (verticale) coincidente con xz (ed anche yz!) ed un piano di riflessione (verticale) con traslazione di ½ c e contenente la bisettrice di un sestante del piano xy (a 30° dall’asse x).F d 3 m è un gruppo cubico (centrico), che contiene ben 192 operazioni di simmetria. Il reticolo è Cubico a facce centrate (F), esistono piani di scorrimento di tipo ‘diamond’, assi ternari lungo le diagonali di corpo e piani di riflessione m che normali alle diagonali di faccia. Tutte le altre operazioni di simmetria sono generate dalle varie combinazioni di F, d, 3 ed m.
Il numero di punti equivalenti nella cella unitaria è chiamata molteplicità. Essa equivale al numero di operazioni di simmetria del gruppo.
Una posizione generale è un gruppo di punti equivalenti con simmetria puntuale (simmetria di sito) 1. Ovvero nessuna!
Una posizione speciale è un gruppo di punti equivalenti con simmetria puntuale (simmetria di sito) maggiore di 1.
L’unità asimmetrica di un gruppo spaziale è la più piccola parte della cella che, attraverso le operazioni di simmetria di gruppo, riempie completamente la cella stessa. I suo volume è dato da:
V(unità asim.) = V(cella)/molteplicità della posizione generale
All’interno dell’unità asimmetrica NON esiste alcuna coppia di punti correlata da un’operazione di simmetria del gruppo.
L’unità asimmetrica contiene TUTTA l’informazione necessaria per la descrizione della struttura cristallina, una volta noti il gruppo spaziale e la cella.
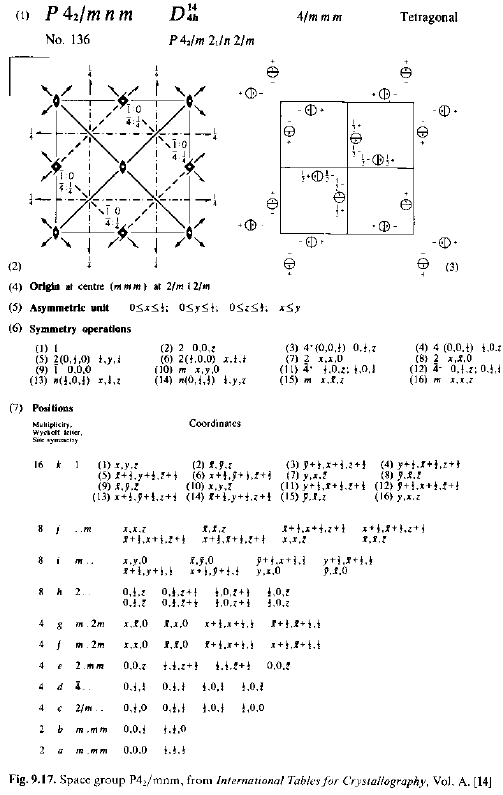
Come si leggono le Tabelle Internazionali?
(1) Simbolo Gruppo Spaziale (H-M), Simbolo Schönflies, gruppo puntuale, sistema cristallino, numero d’ordine, simbolo esteso;
(2) Proiezione degli elementi di simmetria sul piano xy con a verticale e b orizzontale, origine in alto a sinistra;
(3) Proiezione di una posizione generale sul piano xy, con indicazione della coordinata z e della chiralità (,);
(4) Scelta dell’origine della cella rispetto agli elementi di simmetria;
(5) Indicazione dell’unità asimmetrica;
(6) Le operazioni di simmetria del gruppo spaziale;
(7) Molteplicità della posizione, ‘posizione di Wyckoff’ (ordine antialfabetico), la simmetria di sito (gruppo puntuale), coordinate dei punti equivalenti.
Portale "Ingegneria e
Campanologia" -
Autore -
Sommario
- Mappa del Sito -
Home
Bib-TS-081 - Prof. N. Masciocchi - Dispense del Corso di Laurea in Chimica - Insegnamento di strutturistica chimica
Bib-TS-082 - C.Hammond - The Basics of Crystallography and Diffraction - Ed. International Union of Crystallography and Oxford University Press, 240 pg. (Ed. italiana: Zanichelli)
Bib-TS-083 - J.P.Glusker & K.N.Trueblood - Crystal Structure Analysis: A Primer - Oxford University Press, 220 pg. (non tradotto).